ARITMETICA DEL COMPUTADOR

ARITMÉTICA DEL COMPUTADOR 

El lenguaje usado por las computadoras está basado en unos y ceros ósea el sistema binario y otros sistemas como el octal, hexadecimal.

SISTEMA BINARIO

SUMA

En esta suma binaria tenemos que tener siempre en mente el resultado de las diversas formas de sumar, y estas son 4:


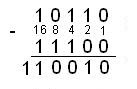
ejemplo:

para comprobar la operación a las cifras las elevamos con base 2 comenzando de derecha a izquierda, a la base 2 le agregamos exponente desde 0 (cero)

a cada base le realizamos la operación del exponente.


obteniendo el resultado de los exponentes, sumamos solo el resultado de los "1" ignorando a los ceros.


para verificar el resultado debemos de realizar los mismos pasos y el resultado que obtengamos debe ser el mismo resultado de la suma de los dos resultados anteriores.

RESTA

La resta binaria es mus sencilla de realizar, podríamos decir que es idéntica a las restas normales.

Como a cero no le puedo restar 1 se le pide "prestado” al 1 mas cercano que este del cero hacia la izquierda y el cero se convierte en dos y al 1 que le pedí “prestado” se convierte en cero.

Para comprobar el resultado se realizan los mismos pasos de la suma solo que para el resultado final se restan.

Solo a los resultados de los “unos” los sumamos ignorando a los de los “ceros”

El resultado se resta y si es igual al de abajo la respuesta será correcta.

MULTIPLICACION

la multiplicación binaria es igual a las demás multiplicaciones solo que a la hora de sumar los resultados es igual que la suma binaria.

Para comprobar realiza los demás pasos de la suma binaria.
Si el resultado final sale igual al resultado de la multiplicación la operación esta correcta.

DIVICION

La división es igual a las demás divisiones.

Primero verificamos en cuantos dígitos cave el divisor

Después coloca un 1 sobre el último digito de la cifra en la cual cave tu divisor.
Enseguida multiplica el uno por cada digito del divisor.

Lo que colocas en el interior, réstalo.

Si el divisor no cave en tu resultado baja otro digito o cuantos sean necesarios para que puedas seguir la operación.

Igual que el primer paso multiplica el 1 por la cifra exterior

Para comprobar tu operación, multiplica el resultado por la cantidad exterior, multiplícalo de forma binaria.

Suma el resultado obtenido de forma binaria.

Al resultado de la multiplicación súmale el residuo de la división de forma binaria.

Si el resultado es igual al dividendo la operación esta correcta.


TRANFORMAR UN DECIMAL A BINARIO

Para transformar un binario a decimal se divide para 2 y el cociente obtenido de nuevo se sigue dividiendo para 2 y así sucesivamente se repite hasta que el cociente resultante sea menor que 2.
Por último se escribe, por este orden el último cociente, el último resto, el penúltimo resto, el antepenúltimo resto,...
El número 545 en base 2 es 1000100001.

TRANFORMAR UN BINARIO A DECIMAL

Para transformar un binario a decimal se procede de la siguiente manera:

Por ejemplo:

1 1 0 0 = 1*(2^3)+1*(2^2)+0*(2^1)+0*(2^0)=8+4=12
2^3 2^2 2^1 2^0


SISTEMA OCTAL
 



El sistema octal es también usado en la computación por tener una base que es potencia exacta de 2 o de la numeración binaria. Esta característica hace que la conversión a binario o viceversa sea bastante simple. El sistema octal usa 8 dígitos (0,1,2,3,4,5,6,7) y tienen el mismo valor que en el sistema de numeración decimal.

Ejemplo:

2568

8*(8^0) + 6*(8^1) + 5*(8^2) + 2*(8^3) = 8 + 48 + 320 + 1024=1400

SISTEMA HEXADECIMAL

Los números hexadecimales son como los números decimales hasta el 9, pero se usan letras ("A',"B","C","D","E","F") para los valores 10 a 15:

Decimal: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Hexadecimal: 0 1 2 3 4 5 6 7 8 9 A B C D E F

EJEMPLO:

2B
2*(16^1) + B*(16^0) = 2*16 + B*1 = 32+B=> (B=11) => 43